들어가기전,
오차와 잔차의 정의를 알고 시작하자!!
예측값 : 만들어진 모델이 추정하는 값 (보통y)
잔차 : 표본집단에서의 예측값과 관측값 차이
오차 : 모집단에서의 예측값과 관측값 차이
www.kaggle.com/c/house-prices-advanced-regression-techniques/overview
House Prices - Advanced Regression Techniques
Predict sales prices and practice feature engineering, RFs, and gradient boosting
www.kaggle.com
목표 : 주택 판매 가격 예측!
선형회귀로 예측을 하기전에 해야할 것이 있다.
1. 통계정보를 활용하기 - 가장 간단하고 직관적인 방법
df[ ].min()
df[ ].max()
df[ ].mean()
df[ ].median()
# SalePrice의 최소, 최대, 평균, 중앙값 계산
df['SalePrice'].min(), df['SalePrice'].max(), df['SalePrice'].mean(), df['SalePrice'].median()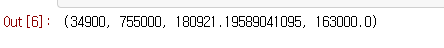
## SalePrice 통계 정보를 요약해서 확인할 수도 있습니다.
df['SalePrice'].describe()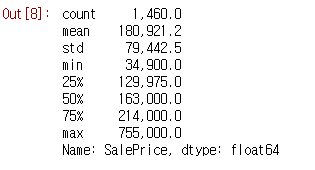
import matplotlib.pyplot as plt
import seaborn as sns
## SalePrice의 확률밀도함수를 그려보겠습니다
sns.displot(df['SalePrice'], kde=True)
## 평균과, 중간값으로 수직선을 그려보겠습니다.
plt.axvline(df['SalePrice'].mean(), color='blue')
plt.axvline(df['SalePrice'].median(), color='red');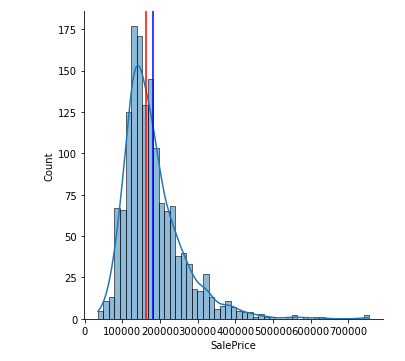
2. 기준모델 정하기 - 가장 간단하면서도 최소한의 성능을 나타내는 기준이 되는 모델
- 분류문제: 타겟의 최빈 클래스
- 회귀문제: 타겟의 평균값
- 시계열회귀문제: 이전 타임스탬프의 값
보통 이렇게 설정한다.
나는 평균값으로 기준모델을 설정하였다.
## predict: 우리가 정한 기준모델인 평균으로 예측을 합니다
predict = df['SalePrice'].mean()## 평균값으로 예측할 때 샘플 별 평균값과의 차이(error)를 저장합니다
errors = predict - df['SalePrice']error를 구하는 이유는 MAE(Mean Absolute Error, 평균절대오차)를 구하기 위해서 이다.
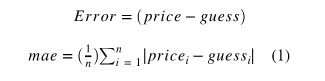
x = df['GrLivArea']
y = df['SalePrice']
predict = df['SalePrice'].mean()
errors = predict - df['SalePrice']
mean_absolute_error = errors.abs().mean()
sns.lineplot(x=x, y=predict, color='red')
sns.scatterplot(x=x, y=y, color='blue');
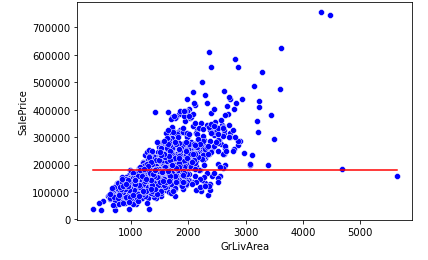
print(f'예측한 주택 가격이 ${predict:,.0f}이며 절대평균에러가 ${mean_absolute_error:,.0f}임을 확인할 수 있습니다.')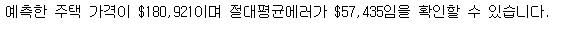
평균 예측은 에러가 상당히 크다는 것을 직관적으로 알 수 있다!!
그 뒤 특성들의 상관관계를 순차적으로 알아본뒤, 영향력있는 주요 변수를 추리는 과정을 거치면 된다.
sns.set(style='whitegrid', context='notebook')
cols = ['GrLivArea', 'LotArea','SalePrice']
sns.pairplot(df[cols], height=2);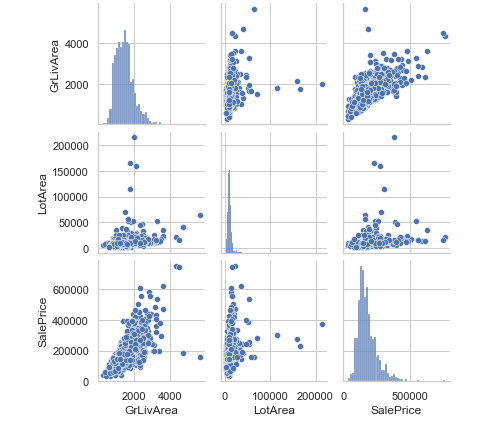
예측모델(Predictive Model)
회귀전은 잔차 제곱들의 합인 RSS(rediual sum of square)를 최소화 하는 직선
RSS는 SSE(Sum of square Error) 라고 하며 == 비용함수 (Cost function)이라고도 한다.
머신러닝은 비용함수를 최소화 하는 모델을 찾는 과정을 학습이라고 한다.
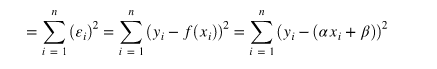
이렇게 잔차제곱합을 최소화하는 방법을 최소제곱회귀 혹은 Ordinary least squares(OLS)라고 부른다.
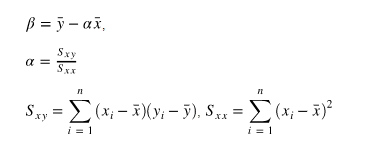
## Seaborn regplot으로 그리면,
sns.regplot(x=df['GrLivArea'], y=df['SalePrice']);reg = regression
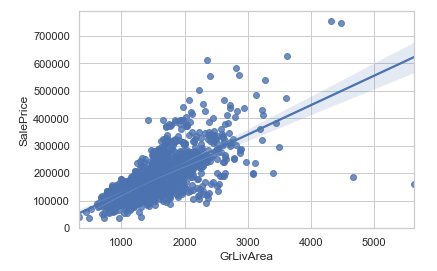
이렇게 회귀선을 그릴수가 있다. 그럼 우리는 위와 같은 것을 예측모델이라 할 수 있을까? ?
정답은 !! NO!!
새로운 sample을 가져왔을 때, 새로운 sample에 대한 예측이 불가능하기 때문에 회귀선에 불가하다.
그럼 어떻게 모델을 만들까.
바로 scikit-learn을 사용해서이다!
## Scikit-Learn 라이브러리에서 사용할 예측모델 클래스를 Import 합니다
from sklearn.linear_model import LinearRegression## 예측모델 인스턴스를 만듭니다
model = LinearRegression()## X 특성들의 테이블과, y 타겟 벡터를 만듭니다
feature = ['GrLivArea']
target = ['SalePrice']
X_train = df[feature]
y_train = df[target]## 모델을 학습(fit)합니다
model.fit(X_train, y_train)## 새로운 데이터 한 샘플을 선택해 학습한 모델을 통해 예측해 봅니다
X_test = [[4000]]
y_pred = model.predict(X_test)
print(f'{X_test[0][0]} sqft GrLivArea를 가지는 주택의 예상 가격은 ${int(y_pred)} 입니다.')
## 전체 테스트 데이터를 모델을 통해 예측해 봅니다.
X_test = [[x] for x in df_t['GrLivArea']]
y_pred = model.predict(X_test)## 전체 예측값 입니다.
y_pred## train 데이터에 대한 그래프를 그려보겠습니다.
plt.scatter(X_train, y_train, color='black', linewidth=1)
## test 데이터에 대한 예측을 파란색 점으로 나타내 보겠습니다.
plt.scatter(X_test, y_pred, color='blue', linewidth=1);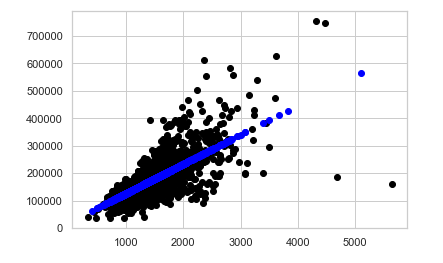
'Data analysis > Data Process' 카테고리의 다른 글
| 데이터 기본 전처리 (결측치 제거 , 데이터 타입 / Python)jupyter notebook, Colab (3) | 2021.04.08 |
|---|---|
| Category_encoders / ML in Python / 범주형 변수 변환 (0) | 2021.02.15 |
| Simple Regression/ 선형회귀(Linear Regression) (0) | 2021.02.14 |
| Matrix Calculation(Matrix multiplication)/행렬의 연산 Python으로 구현하기 (0) | 2021.01.13 |
| 선형대수 in AI (벡터와 매트릭스vectors and Matrices)/python 파이썬 (0) | 2021.01.13 |
